Ya que estamos próximos al estreno del capítulo final del manga de Shingeki no Kyojin (Attack on Titan), me pareció buen momento para compartir un problema geométrico que me vino a la mente cuando empecé a ver el anime por allá en el 2014.

Contexto #

En esta serie, la humanidad* es asediada por seres gigantes, violentos y de aparente escasa inteligencia llamados los titanes. Por esto, se ven obligados a vivir encerrados dentro de un gran complejo amurallado, compuesto de tres murallas concéntricas. La figura que muestran en la serie es la siguiente:

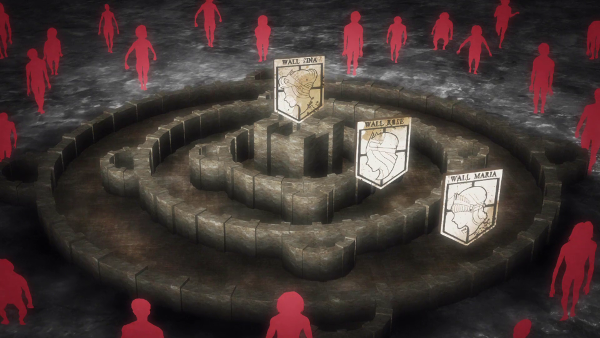
* No spoilers

El problema #

Así ha sobrevivido la humanidad durante los últimos 100 años. Sin embargo, todo cambia un día: aparecen un titán gigante y un titán acorazado que logran abrir un hueco en la muralla exterior, permitiendo la entrada de titanes a la ciudad.

Con titanes dentro se desata el caos. La humanidad se ve obligada a replegarse dentro de las dos murallas restantes, no sin antes sufrir una gran cantidad de muertes.

Y aquí viene el problema: en el capítulo 12 del anime, se menciona que en este ataque la humanidad perdió “un tercio de su territorio”. Cuando vi esto, me pareció que no podía ser cierto.

Yo imaginaba las murallas como tres círculos concéntricos con radios $r_1 = 1$, $r_2 = 2$ y $r_3 = 3$.

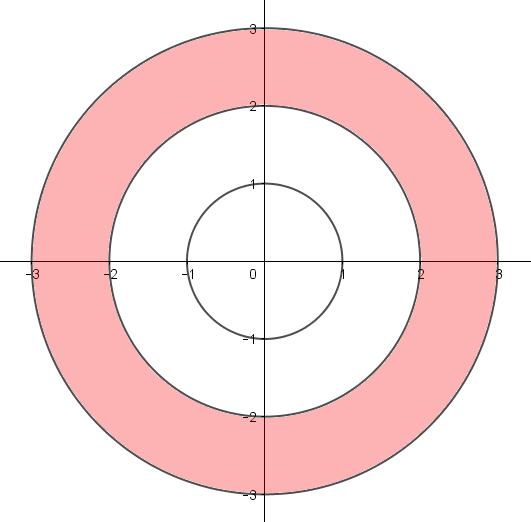
En geometría, la figura delimitada por dos circunferencias concéntricas (por ejemplo, lo señalado en rojo en la figura anterior) se llama corona circular.

Viendo este esquema de las murallas, no me pareció posible que el área de la corona circular exterior correspondiera a $\frac{1}{3}$ del área total. Pensé que debía ser una fracción mayor. Hagamos los cálculos:

$$ A_{total} = \pi (r_3)^2 $$

$$ A_{exterior} = \pi (r_3)^2 - \pi (r_2)^2 $$

$$ \frac{A_{exterior}}{A_{total}} = \frac{\pi (r_3)^2 - \pi (r_2)^2}{\pi (r_3)^2} $$

Reemplazando los valores de $r_2 = 2$ y $r_3 = 3$ nos queda que:

$$ \frac{A_{exterior}}{A_{total}} = \frac{5 \pi}{9 \pi} = \frac{5}{9} \approx 0.55 $$

Esto significa que, en realidad, ¡el territorio perdido en el ataque sería más de la mitad del total!

Pero claro, no sé cual es la proporción real de los radios de las murallas. Este resultado se basa apenas en una estimación que hice a ojo.

Podemos decir entonces que, o las proporciones mostradas en la serie no son muy precisas, o no hice bien mi estimación, o al autor le fallaron los cálculos y en realidad la humanidad perdió más de la mitad de su territorio.

Un paso más #

Luego llevé el problema un paso más allá: ¿cuál debe ser la proporción de los radios para que el área de la corona circular exterior sea igual a $\frac{1}{3}$ del área total?

Notemos que el valor de $r_1$ realmente no importa. Lo importante es la relación entre $r_2$ y $r_3$. Partiendo de la ecuación que derivamos anteriormente, encontremos el valor de $r_3$ que hace que esta expresión sea igual a $\frac{1}{3}$.

$$ \frac{A_{exterior}}{A_{total}} = \frac{\pi (r_3)^2 - \pi (r_2)^2}{\pi (r_3)^2} = \frac{1}{3} $$

$$ 3 \left( \pi (r_3)^2 - \pi (r_2)^2 \right) = \pi (r_3)^2 $$

$$2 \pi (r_3)^2 = 3 \pi (r_2)^2 $$

$$ 2 \pi (r_3)^2 = 3 \pi (r_2)^2 $$

$$ r_3 = \sqrt{1.5} \cdot r_2 $$

Esto quiere decir que, si mantenemos nuestro valor de $r_2 = 2$, entonces:

$$ r_3 = \sqrt{1.5} \cdot 2 \approx 2.45 $$

Con estos valores de $r_2$ y $r_3$, y agregando nuevamente a $r_1 = 1$ para tener la figura completa, quedaría así:

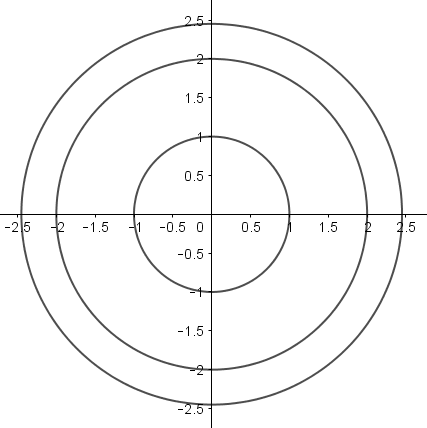
Las proporciones se ven muy diferentes a la imagen de la serie. La corona circular exterior es mucho más estrecha.