Mi historia #

Cuando tenía unos 10 u 11 años, un amigo del colegio me retó a que no era capaz de dibujar la siguiente figura sin levantar el lápiz de la hoja ni pasar dos veces por la misma línea:

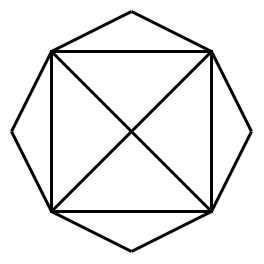
A mi me gustaban ese tipo de problemas así que le dediqué un buen rato, pero por más que lo intentaba siempre me quedaba faltando una línea. Después de un rato finalmente mi amigo me reveló que todo había sido un truco: dibujar la figura con esas condiciones es una tarea imposible. Aunque no me dio ninguna explicación de por qué era imposible, yo lo había intentado tanto y de tantas formas que le creí sin más. Y quedé muy asombrado por el hecho de que una tarea en apariencia tan simple no se pudiera lograr.

Unos dos o tres años después volví a encontrarme con el problema en un libro que cayó en mis manos. Cuando lo vi dije, ¡ah, esta ya me la sé, no se puede lograr! Grande fue mi sorpresa cuando fui a mirar en la parte de atrás del libro, donde estaban las soluciones a las preguntas, y me encontré con que sí había una manera de dibujar la figura con esas condiciones. Pero había una trampa: para lograrlo había que doblar la esquina de la hoja de papel, así:

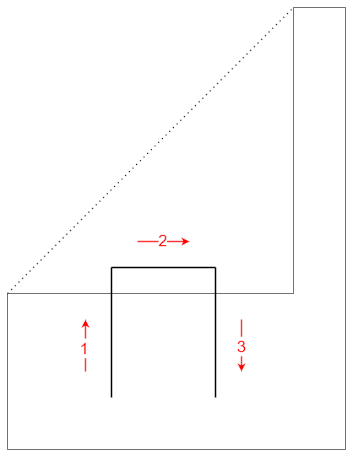
Luego desdoblamos la hoja y completamos la figura fácilmente:

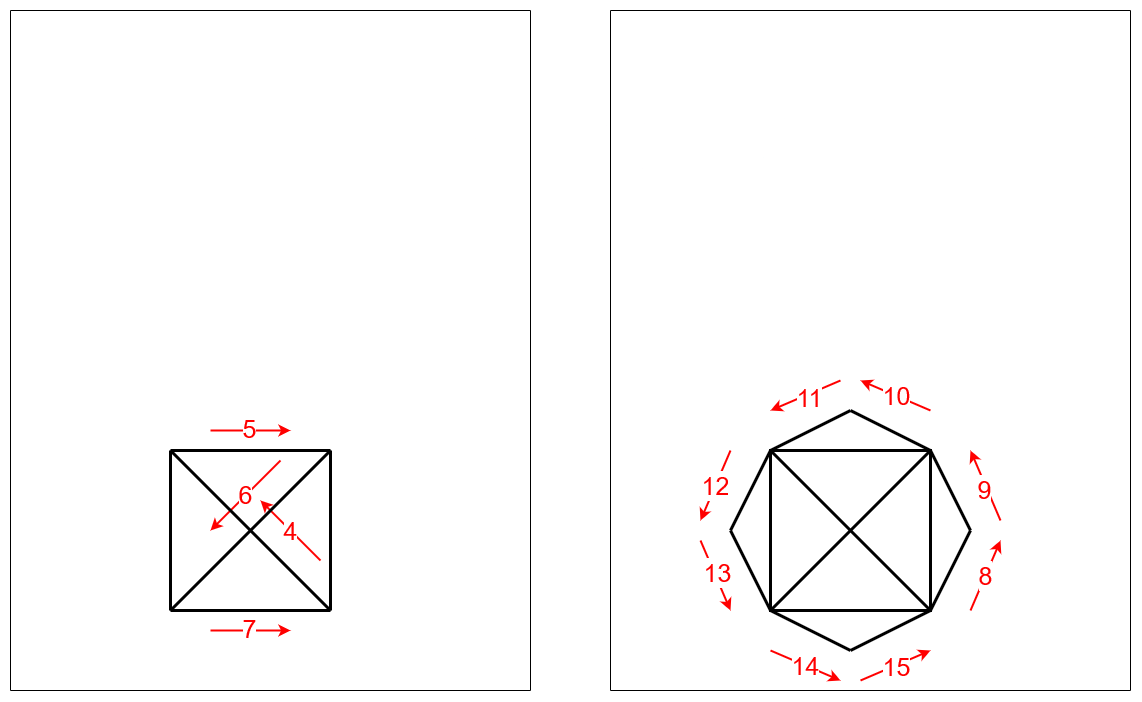
Esto me pareció muy ingenioso, y además me reafirmó en que la tarea original sí era imposible, ya que si existiera una solución legal el libro la presentaría en lugar de la solución con trampa.

Sin embargo, para llegar a la explicación de por qué era imposible tuvieron que pasar varios años más. Ya estando en la universidad conocí los algoritmos, las matemáticas discretas y en especial la teoría de grafos, temas que me apasionaron por esa época. Y fue allí donde finalmente pude conocer la respuesta al misterio.

La historia del problema #

Resulta pues que por el siglo XVIII en la ciudad de Königsberg (hoy Kaliningrado) había 7 puentes que cruzaban el río y conectaban diferentes islas. La gente se preguntaba si había una forma de hacer un recorrido que pasara por cada puente una sola vez. Pero por más que lo intentaban nadie podía dar con dicho recorrido.

Entonces a alguien se le ocurrió preguntarle a uno de los matemáticos más importantes no sólo de la época, sino de la historia: Leonhard Euler. Este señor, ni corto ni perezoso, se puso a analizar el problema, y no sólo demostró que el recorrido era imposible, sino que para ello se inventó él solito toda una nueva rama de las matemáticas: la teoría de grafos.

Empecemos por dibujar la figura de los puentes como lo que los matemáticos llaman un grafo. Cada “pedazo de tierra” (A,B,C,D en la figura) lo representamos con un punto (vértice), y cada puente que une dos vértices lo representamos con una línea (arista).

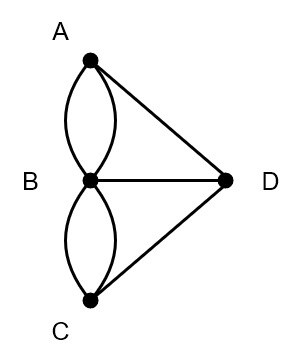
¿Y qué tiene que ver el problema de los puentes con la figura que mencioné al principio? Pues que el problema de hacer un recorrido por los puentes es equivalente al problema de dibujar su grafo sin levantar el lápiz ni repetir aristas. Imagina que en el papel están dibujados ya los vértices, y cada vez que cruzamos un puente en nuestro recorrido, trazamos la arista correspondiente en el grafo.

La solución #

Pues bien, Euler demostró que el recorrido sólo es posible si el grafo tiene 0 o 2 vértices con un número impar de aristas (en jerga matemática diríamos que el vértice tiene un grado impar).

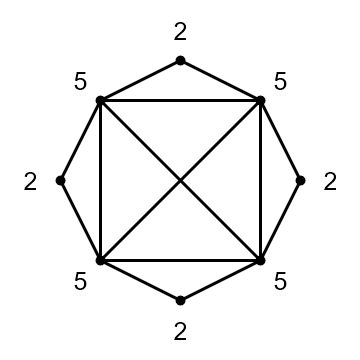
Si revisamos el grafo de los puentes de Königsberg nos damos cuenta de que los 4 vértices tienen un número impar de aristas, por lo tanto en este caso el recorrido es imposible:

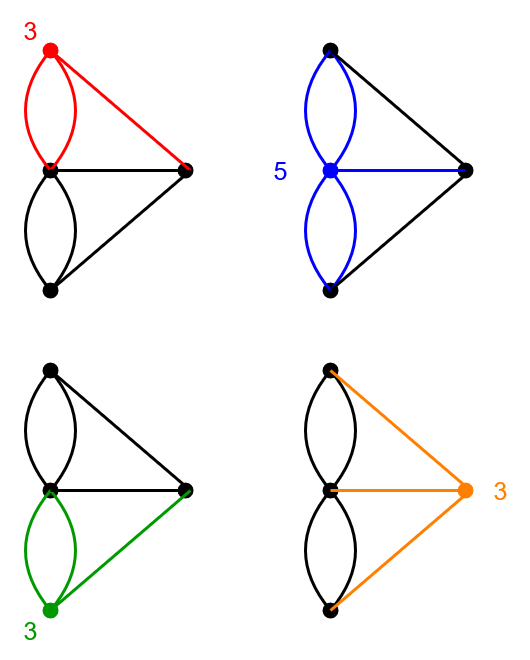
Si hacemos lo mismo con la figura que mencioné al inicio veremos que hay 4 vértices con grado impar. He aquí, ¡por fin!, la explicación de por qué es imposible dibujar la figura sin levantar el lápiz ni repetir aristas.

Muy bien, pero el lector agudo se dará cuenta de que no hemos presentado la demostración del teorema. Es decir, ¿de dónde saca Euler que sólo se puede lograr si 0 o 2 vértices tienen grado impar? Un esbozo de demostración es que siempre que entramos a un vértice tenemos que salir de él, excepto cuando es el último vértice visitado. Si el grado del vértice es par significa que hay un número igual de “entradas” y de “salidas”. Pero si es impar, llega a un punto donde entramos a un vértice y ya no podemos volver a salir, o salimos y ya no podemos volver a entrar. Si el grafo tiene 2 vértices con grado impar, podemos iniciar nuestro recorrido en uno y terminarlo en el otro. Pero si tiene más de 2, inevitablemente entraremos a un vértice con grado impar del que ya no podremos salir, dejando el dibujo incompleto. En este video se explica un poco mejor.

Epílogo #

Durante la Segunda Guerra Mundial dos de los puentes fueron bombardeados, por lo cual la cosa quedo así:

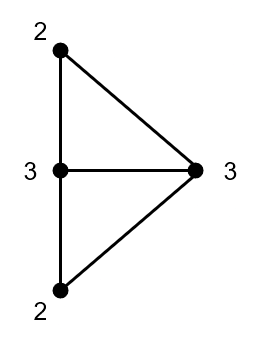
Ahora el recorrido sí es posible, ya que sólo hay 2 vértices con número impar de aristas.