En el municipio de La Unión, Antioquia, hay un estadero llamado El Edén, parada común de los viajeros que se dirigen hacia Sonsón o Argelia. Allí venden algo que no he visto en ningún otro lugar: un buñuelo en forma de rosca.

La verdad no sé por qué lo hacen de esta manera. Puede ser simplemente por ofrecer algo novedoso y diferente, quizá buscando que la gente lo compre por curiosidad.
Sin embargo, tengo una hipótesis. ¿Será que un buñuelo en forma de rosca tiene más “cubierta” que un buñuelo normal hecho con la misma cantidad de masa? De ser cierto, considero que el buñuelo en forma de rosca tendría una verdadera ventaja frente al buñuelo redondo normal (aunque para la gente a la que no le gusta la cubierta del buñuelo sería todo lo contrario).
Vamos a averiguarlo.
En términos matemáticos #
En matemáticas, esa forma de “rosca” se llama toro (curioso nombre), y un buñuelo normal tendría forma de esfera. La “cubierta” del buñuelo sería el área, y la “cantidad de masa” sería el volumen.
La pregunta es, ¿dos objetos con el mismo volumen pueden tener diferente área? La respuesta es sí, y en lugar de alargar el post con un ejemplo cualquiera, comprobémoslo con el mismo buñuelo.
La esfera #
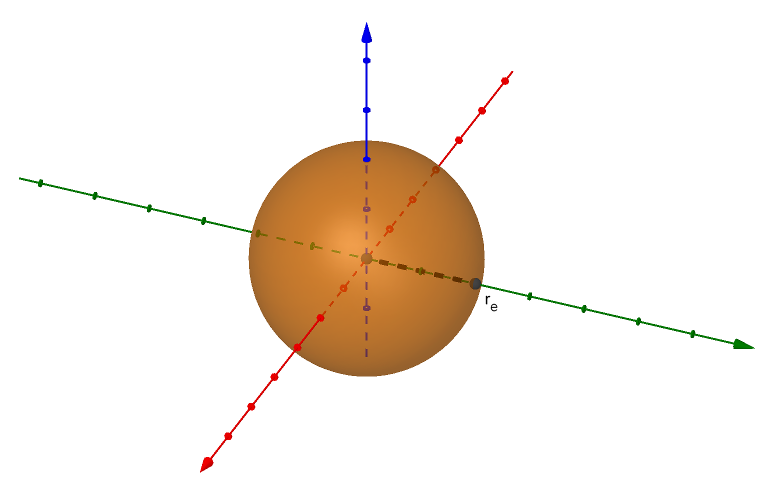
$$ V_e = \frac{4}{3} \pi {r_e}^3 $$
El toro #
Los parámetros que definen al toro son dos radios:
- El mayor: va desde el centro del toro al centro del “tubo”
- El menor: el radio del “tubo”
Los llamaré $r_a$ y $r_b$ respectivamente. En la siguiente imagen de un toro “recortado” (alguien le metió un mordisco al buñuelo), se aprecian ambos radios.
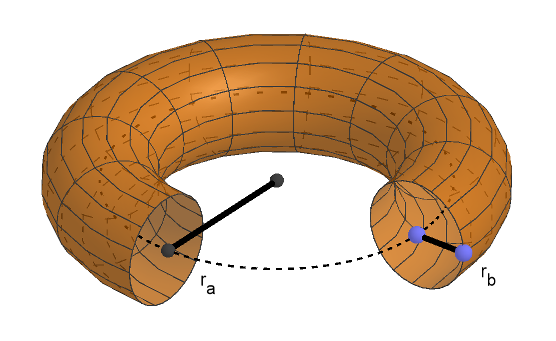
Para simplificar el análisis, voy a estimar a ojo que el radio mayor del buñuelo es 3 veces el radio menor ($r_a = 3 r_b$). Siendo así, el área y el volumen nos quedan: $$ A_t = 4 \pi^2 r_a r_b = 4 \pi^2 (3 r_b) r_b = 12 \pi^2 {r_b}^2 $$
$$ V_t = 2 \pi^2 r_a {r_b}^2 = 2 \pi^2 (3 r_b) {r_b}^2 = 6 \pi^2 {r_b}^3 $$
Calculando #
Vamos a igualar el volumen de ambos para hallar el radio del toro en términos del de la esfera. $$ V_e = V_t $$
$$ \frac{4}{3} \pi {r_e}^3 = 6 \pi^2 {r_b}^3 $$
$$ \frac{4}{18 \pi} {r_e}^3 = {r_b}^3 $$
$$ \sqrt[3]{\frac{2}{9 \pi}} r_e = r_b $$
Lo que quiere decir esto es que dada una esfera cualquiera de radio $r_e$, un toro con radio menor $r_b = \sqrt[3]{\frac{2}{9 \pi}} r_e$ (y con radio mayor $r_a = 3 r_b$) tendrá el mismo volumen.
Ahora, utilizando este radio, encontremos el área de dicho toro: $$ A_t = 12 \pi^2 {r_b}^2 = 12 \pi^2 (\sqrt[3]{\frac{2}{9 \pi}} r_e)^2 $$
Y si comparamos las dos áreas: $$ \frac{A_t}{A_e} = \frac{12 \pi^2 (\sqrt[3]{\frac{2}{9 \pi}} r_e)^2}{4 \pi {r_e}^2} = 3 \pi (\sqrt[3]{\frac{2}{9 \pi}})^2 \approx 1.612 $$
Esto quiere decir que ¡un buñuelo en forma de toro tiene un $61%$ más de cubierta que un buñuelo normal hecho con la misma cantidad de masa!